Question

Farmer Ed has 150 meters of fencing and wants to enclose a rectangular play that borders a river. If farmer Ed does not fence in the side along the river, find the length and width of the plot that will maximize the area. What is the largest area that can be enclosed?

Answer 1

To maximize the area of a rectangular plot with 150 meters of fencing along three sides, Farmer Ed should use dimensions of 37.5 meters for width and 75 meters for length, resulting in a maximum area of 2812.5 square meters.

Step-by-step explanation:

Optimizing Area with a Given Amount of Fencing

Farmer Ed has 150 meters of fencing to enclose a rectangular plot of land that borders a river. Since the river acts as a natural barrier, he will not use fencing on that side. To find the dimensions of the plot that will maximize the area, we can use calculus or reasoning based on the properties of rectangles.

Let's denote the width of the rectangle that will be fenced as W and the length as L. Because two widths and one length will be fenced, we know that 2W + L = 150 meters. This implies that L = 150 - 2W. The area A to be maximized is A = W * L. By substituting the expression for L, we get A = W(150 - 2W), which simplifies to A = 150W - 2W^2.

To find the maximum area, we take the derivative of A with respect to W and set it to zero: dA/dW = 150 - 4W = 0. Solving this, we find that W = 37.5 meters. The corresponding length L is then 150 - 2(37.5) = 75 meters. Thus, the rectangle with maximum area has dimensions of 37.5 meters by 75 meters, and the maximum area that can be enclosed is 2812.5 square meters.

Answer 2

The largest area will be 2812.5 square meters.

Step-by-step explanation:

The perimeter of rectangle is given as:

`2L+2W` (L is the length and W is the width)

As one side is not to be fenced, so the formula here will be :
`P=L+2w`

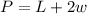
Perimeter is 150.

So,
`150=L+2W` ;
`L=150-2W`

Area of the rectangle is :
`LW`

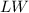
Plugging the value of L in the area formula;

Area =
`(150 -2W)(W)`

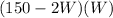
This is a parabola or quadratic function whose maximum or minimum values occur at the average of the solutions.

So, Solving
`(150 -2W)(W)=0`

=>
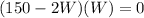
`150 -2W = 0` Or
`W=0`

=>
`150-2W=0`

=>
`2W=150`

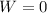
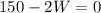
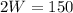
W = 75

So, the two solutions are zero and 75.

The average of them is
`(0+75)/(2)=37.5`

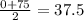
Now, the maximum area is at W=37.5

And
`L=150-2(37.5)`

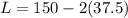
L = 75

The dimensions that maximize the area are L=75 and width W=37.5

And maximum area =
`75*37.5` = 2812.5 square meters

Hence, the largest area will be 2812.5 square meters.