Question

The tool life decreases from 0.8 min to 0.2 min due to the increase in cutting speed from 60 m/min to 120 m/min in a turning operation.

Compute is the value of the cutting speed at 0.4 min.

a-)Determine the spindle speed in rpm.

b-)Find the required power for the unit force.

c-)The friction between tool and workpiece varies 0.25-0.35 during the process.
d-)Calculate the rate of maximum force to minimum force.

Answer 1

The value of the cutting speed = 84.85 m/min

a.)The value of the spindle speed = 270.08 rpm

b.)The value of the Power for the unit force = 1.414 W

c.)
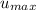`u_(max)` = 0.35,
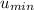`u_(min)` = 0.25

d.)The rate of maximum force to minimum force = 1.4

Step-by-step explanation:

As given, T₁ = 0.8 min

T₂ = 0.2 min

V₁ = 60 m/min

V₂ = 120 m/min

Now, as we know that Taylor's tool life equation -

VTⁿ = k

where V = speed in m/min

T = time in min

n = Index

k = constant

Now,

V₁T₁ⁿ = V₂T₂ⁿ

⇒60 (0.8)ⁿ = 120(0.2)ⁿ

⇒ (0.8)ⁿ = 2(0.2)ⁿ

⇒ (
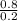`(0.8)/(0.2)` )ⁿ = 2

⇒4ⁿ = 2

Taking log both side , we get

⇒n log(4) = log(2)

⇒n =
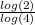`(log(2))/(log(4))` = 0.5

Now,

As given , T = 0.4 min

We know,

VTⁿ = V₁T₁ⁿ

⇒V (0.4)ⁿ = 60(0.8)ⁿ

⇒V = 60(
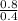`(0.8)/(0.4)` )ⁿ

⇒V = 60(2)ⁿ

⇒V = 60(
`2^(0.5)`)

⇒V = 84.85 m/min

∴ The value of the cutting speed = 84.85 m/min

a.)

As we know ,

V = π×d×N

Let d = 100 mm = 0.1 m

⇒ 84.85 = π×0.1×N

⇒ N =
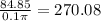`(84.85)/(0.1\pi ) = 270.08` rpm

∴ The value of the spindle speed = 270.08 rpm

b.)

As we know,

P = F×V

⇒P = 1×
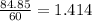`(84.85)/(60) = 1.414` W per unit force

∴ The value of the Power for the unit force = 1.414 W

c.)

As given - The friction between tool and workpiece varies 0.25-0.35 during the process.

⇒
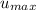`u_(max)` = 0.35

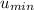`u_(min)` = 0.25

d.)

Rate of maximum force ,
`F_(max)` =
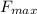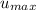`u_(max)` × Normal force

Rate of minimum force ,
`F_(min)` =
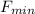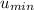`u_(min)` × Normal force

∴ we get

`(F_(max) )/(F_(min) ) = (u_(max) )/(u_(min) ) = (0.35)/(0.25)` = 1.4

∴ we get

The rate of maximum force to minimum force = 1.4