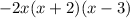The expression we have is:
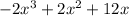
To factor this expression we need to identify the common elements in the terms.
We can see that the variable x is present in all of the terms, so we will factor the x with the lowest exponent. In this case that is "x".
Also, to factor, we need to look at the coefficients (the numbers beside the variables) and check if they are multiples of the same number. In this case, -2, 2, and 12 are multiples of 2.
Thus, the common term is 2x (we combine the number and variable that are common to all the terms)
Before we factor, we express each term as multiplication by 2x
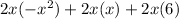
Now, we factor the common term 2x, and we leave inside a parenthesis the remaining terms:
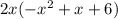
We can also leave out the "-" sign by inverting the signs inside:
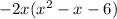
Next, we factor again but we only take the expression inside the parenthesis to factor:
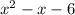
We factor this by looking for two numbers that when added result in the coefficient of x (-1) and when multiplied result in the independent term (-6).
Those numbers are 2 and -3, because 2-3=-2 and (2)(-3)=-6
So the factorization is:
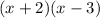
We substitute this in the previous expression for the factorization:
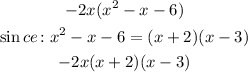
Answer: