Question

A geometric sequence is defined recursively by an = 6an -1 . The first term of the sequence is 0.75. Which of the following is the explicit formula for the nth term of the sequence?

Answer 1

Hello,


`u_(1)= (3)/(4) \\ u_(2)= (3)/(4)*6^(1) \\ u_(3)= (3)/(4)*6^(2) \\ u_(4)= (3)/(4)*6^(3) \\ ...\\ \boxed{u_(n)= (3)/(4)*6^(n-1) } \\`

Answer 2

The explicit formula for the nth term of the sequence is
`a_n=0.75(6)^(n-1)`.

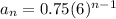Explanation:

The recursive formula of a GP is

`a_n=6a_(n-1)`

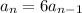
It is given that the first term is 0.75, it means

`a_1=0.75`

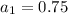
The next terms of GP are

`a_2=6a_(2-1)=6* (0.75)=4.5`

`a_3=6a_(3-1)=6* (4.5)=27`

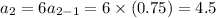
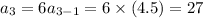
The GP is defined as

`0.75,4.5,27`

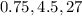
Here the first term is 0.75 and the common ratio is 6.

The explicit formula for the nth term of a GP is

`a_n=ar^(n-1)`

The explicit formula for the nth term of the sequence

`a_n=0.75(6)^(n-1)`

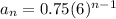
Therefore the explicit formula for the nth term of the sequence is
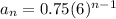`a_n=0.75(6)^(n-1)`.