
Step-by-step explanation
Step 1
a) the wire at 65 ° ( red)
we have a rigth triangle (B) so
let
length of the wire= hypotenuse
angle=65 °
opposite side= 100
hence, we need use a funciton that relates those three values
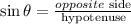
replace

Step 2
now, let's find the distnace x
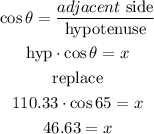
Step 3
now, find wire 2

Step 4
finally, to find the total length of the wire
, add
total length= (wire1+wire2+4+4)*3times
replace

therefore, the answer is

I hope this helps you