Question

4. To hold up a communications tower which is 100 m high, 3 sets of 2 cables (as shown in the diagram) are positioned equally around the tower. Find the total length of cable required if an extra 4 m are needed to fasten each wire.

Answer 1

`\text{total length=}572.62\text{ m}`

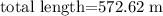
Step-by-step explanation

Step 1

a) the wire at 65 ° ( red)

we have a rigth triangle (B) so

let

length of the wire= hypotenuse

angle=65 °

opposite side= 100

hence, we need use a funciton that relates those three values

`\sin \theta=\frac{opposite\text{ side}}{\text{hypotenuse}}`

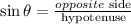
replace

`\begin{gathered} \sin \theta=\frac{opposite\text{ side}}{\text{hypotenuse}} \\ \sin 65=\frac{100}{\text{wire}1} \\ \text{wire}1=(100)/(\sin 65) \\ \text{wire}1=110.33 \end{gathered}`

Step 2

now, let's find the distnace x

`\begin{gathered} \cos \theta=\frac{adjacent\text{ side}}{\text{hypotenuse}} \\ \text{hyp}\cdot\cos \theta=x \\ \text{replace} \\ 110.33\cdot\cos 65=x \\ 46.63=x \end{gathered}`

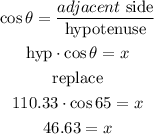
Step 3

now, find wire 2

`\begin{gathered} \text{wire}2\cdot\cos 50=x \\ \text{wire}2=(x)/(\cos 50) \\ \text{wire}2=(46.63)/(\cos 50) \\ \text{wire}2=72.54 \end{gathered}`

Step 4

finally, to find the total length of the wire

, add

total length= (wire1+wire2+4+4)*3times

replace

`\begin{gathered} \text{total length= (110.33+72.54+8)}\cdot3 \\ \text{total length=}572.62\text{ m} \end{gathered}`

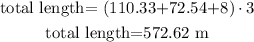
therefore, the answer is

`\text{total length=}572.62\text{ m}`

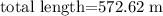
I hope this helps you