Question

Calculate the magnitude of the velocity and the θ angular direction of the block and the bullet together when the 50 g bullet moves to sky at a speed of 600 m/s and hits a sliding 4 kg block with a speed of 12 m/s in a direction with 30o with respect to ground.

Answer 1

Magnitude of the velocity = 16.82 m/s

Angular direction, θ = 52.41°

Step-by-step explanation:

As given ,

mass of bullet, m₁= 50g = 0.05 kg

speed of bullet , u₁ = 600 m/s

mass of the block , m₂ = 4 kg

speed of the block before collision , u₂ = 12 m/s

direction , θ = 30°

Now,

Assume that the combined velocity of bullet and block after collision = v

and the direction = θ

Now, from the conservation of momentum in x - direction :

m₁ u₁ + m₂ u₂ = ( m₁ + m₂ ) vₓ

where v = final velocity after collision

u₁ = initial velocity of bullet before collision = 0

m₁ = mass of the bullet before collision = 0.05 kg

u₂ = velocity of block before collision = 12 cos(30° )

m₂ = mass of block before collision

m₁ + m₂ = combined mass of bullet and block after collision = 0.05 + 4

∴ we get

0.05 (0) + 4(12 cos(30° ) ) = ( 0.05 + 4 ) vₓ

⇒ 0 + 4(6√3) = 4.05 vₓ

⇒24√3 = 4.05 vₓ

⇒vₓ = 10.26 m/s

Now, from the conservation of momentum in y - direction :

m₁ u₁ + m₂ u₂ = ( m₁ + m₂ )
`v_(y)`

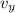
where v = final velocity after collision

u₁= initial velocity of bullet before collision = 600

m₁ = mass of the bullet before collision = 0.05 kg

u₂ = velocity of block before collision = 12 sin(30° )

m₂= mass of block before collision

m₁+ m₂= combined mass of bullet and block after collision = 0.05 + 4

∴ we get

0.05 (600) + 4(12 sin(30° ) ) = ( 0.05 + 4 )
`v_(y)`

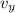
⇒ 30 + 4(6) = 4.05
`v_(y)`

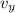
⇒30 +24 = 4.05
`v_(y)`

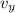
⇒54 = 4.05
`v_(y)`

⇒
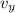
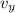`v_(y)` = 13.33 m/s

Now, the magnitude of the velocity = √vₓ² +
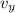`v_(y)`² = √(10.26)² + (13.33)²

= √105.26 + 177.68

= √282.95 = 16.82

The angular direction, θ =
`tan^(-1)`(
`(v_(y) )/(v_(x) )`) =
`tan^(-1)`(
`(13.33)/(10.26)`) =
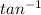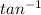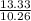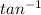`tan^(-1)`(1.299) = 52.41°