Question

please help me work through this, thank you! (also, for part b you substitute before differentiating)

Answer 1

We are given that a pile of sand has the shape of a cone. The volume is given by:

`V=(1)/(3)\pi r^2h`

Where:

`\begin{gathered} r=\text{ radius} \\ h=\text{ height} \end{gathered}`

We are given that the height is 1/4 of the radius. Therefore, we have:

`h=(1)/(4)r`

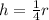
Now, we substitute in the formula for the volume:

`V=(1)/(3)\pi r^2((1)/(4)r)`

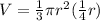
Now, we solve the products:

`V=(1)/(12)\pi r^3`

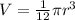
Now, we substitute the value of the radius:

`V=(1)/(12)\pi(12m)^3`

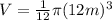
Now, we solve the operations:

`V=452.39m^3`

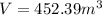
Therefore, the volume is 452.39 cubic meters.

To determine ther rate of change of volume is determined by determining the derivative on both sides of the formula for the volume:

`(dV)/(dt)=(1)/(12)\pi(d)/(dt)(r^3)`

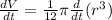
Now, we determine the derivative using the following formula:

`(d)/(dx)(f(x))^n=n(f(x))^(n-1)f^(\prime)(x)`

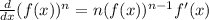
Applying the rule we get:

`(dV)/(dt)=(1)/(12)\pi3r^2(dr)/(dt)`

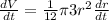
Simplifyiong we get:

`(dV)/(dt)=(1)/(4)\pi r^2(dr)/(dt)`

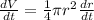
Now, we substitute the values:

`(dV)/(dt)=(1)/(4)\pi(12m)^2(4\text{ m/h\rparen}`

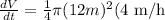
Solving the operations:

`(dV)/(dt)=452.39(m^3)/(h)`

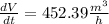
Therefore, the rate of change is 452.39 cubic meters per second.