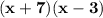Question

Factor by grouping:
vx+7v-3x-21

Answer 1

Solving the expression
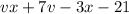`vx+7v-3x-21` using factor by grouping we get
`\mathbf{(x+7)(x-3)}`

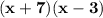
Explanation:

We need to solve the expression
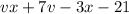`vx+7v-3x-21` using factor by grouping

Factor by grouping requires to group first two terms together and last two terms together and try to find out the common numbers in the groups.

We can group:

`(vx+7v)(-3x-21)`

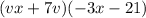
Taking v common from first group and -3 from second

`v(x+7)-3(x+7)`

Taking x+7 common

`(x+7)(x-3)`

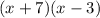
So, Solving the expression
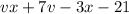`vx+7v-3x-21` using factor by grouping we get
`\mathbf{(x+7)(x-3)}`