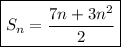Question

An arithmetic sequence has t1=5 and t2=8 find tn and sn

Answer 1

`a_n=2+3n`

`\displaystyle S_n=(7n+3n^2)/(2)`

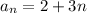
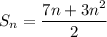
Explanation:

Arithmetic Sequences

The arithmetic sequences are identified because any term n is obtained by adding or subtracting a fixed number to the previous term. That number is called the common difference.

The equation to calculate the nth term of an arithmetic sequence is:

`a_n=a_1+(n-1)r`

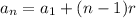
Where

an = nth term

a1 = first term

r = common difference

n = number of the term

The sum of the n terms of an arithmetic sequence is given by:

`\displaystyle S_n=(a_1+a_n)/(2)\cdot n`

We are given the first two terms of the sequence:

a1=5, a2=8. The common difference is:

r = 8 - 5 = 3

Thus the general term of the sequence is:

`a_n=5+(n-1)3=5+3n-3=2+3n`

`\boxed{a_n=2+3n}`

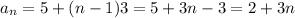
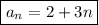
The formula for the sum is:

`\displaystyle S_n=(5+2+3n)/(2)\cdot n`

`\displaystyle S_n=(7+3n)/(2)\cdot n`

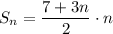
Operating:

`\boxed{\displaystyle S_n=(7n+3n^2)/(2)}`