Answer:
The function
 represents a reflection of
represents a reflection of
 across the y-axis.
across the y-axis.
Explanation:
The given function is

If a function reflected across the y-axis then the sign of x-coordinate is changed but the y-coordinate remain the same.
Mathematically it can be defined as
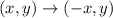
Let function g(x) represents a reflection of f(x) across the y-axis. So, the required function is
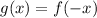

![[\because f(x)=(3)/(8)(4)^(x)]](https://img.qammunity.org/2017/formulas/mathematics/high-school/9ervoin4mbumqhulta8tl84m596qvnseh7.png)
Therefore the function
 represents a reflection of
represents a reflection of
 across the y-axis.
across the y-axis.