Question

List the key features of the quadratic equation y = x2 + 6x - 16.

A. x-intercepts: (-8,0) and (2,0), y-intercept: (0,–16), vertex: (-3,-25).

B. X-intercepts: (-8,0) and (2,0), y-intercept: (0,–6), vertex (-3,-25).

C. X-intercepts: (8,0) and (-2,0), y-intercept: (0.-16), vertex: (-3,-25).

D. x-intercepts: (-8,0) and (2,0), y-intercept: (0,16), vertex: (-3,-25).​

Answer 1

Correct choice is A

Explanation:

Quadratic Function

The vertex form of the quadratic function has the following equation:

`y=a(x-h)^2+k`

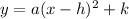
Where (h, k) is the vertex of the parabola that results when plotting the function, and a is a coefficient different from zero.

The x-intercepts are the points where the graph of the function crosses the x-axis, they are also called zeros or roots. They can be found by solving the equation y=0,

The y-intercepts are the points where the graph of the function crosses the y-axis. They can be found by setting x=0.

We are given the function:

`y = f(x)=x^2+6x-16`

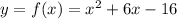
Find the y-intercept. x=0:

`f(0)=0^2+6*0-16=-16`

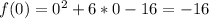
y-intercept: (0,-16)

Find the x-intercepts, y=0. Solve the equation

`x^2+6x-16=0`

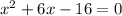
Factoring:

`(x-2)(x+8)=0`

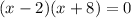
Which gives x=2, x=-8.

X-intercepts (2,0) (-8,0)

This leaves us only choice A as correct. But we'll compute the vertex also.

Completing squares:

`y=x^2+6x-16=x^2+6x+9-16-9=(x+3)^2-25`

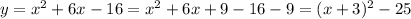
Comparing with the vertex form of the function, we have: h=-3, k=-25, thus the vertex is located at (-3,-25)

This confirms that the correct choice is A