Question

The measure of the height of a triangle is 6 inches less than three times the measure of itsbase. The area of the triangle is 36 square inches. Find both the measures of the height andthe base of the triangle.

Answer 1

`b=6,h=12`

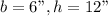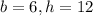
1) Since the height of this triangle is "less than three times the measure of its base" We can call it simply by 3b-6 in which b is the measure of the base.

2) The area is 36 in² so let's plug both pieces of information into the area of a triangle formula and solve it:

`\begin{gathered} A_(\Delta)=(b\cdot h)/(2) \\ 36=(b(3b-6))/(2) \\ 2*36=(b(3b-6))/(2)*2 \\ 72=3b^2-6b \\ 0=3b^2-6b-72 \\ b_=(-\left(-6\right)\pm√(\left(-6\right)^2-4\cdot\:3\left(-72\right)))/(2\cdot\:3) \\ b_1=(-\left(-6\right)+30)/(2\cdot\:3)=(30+6)/(6)=6 \\ b_2=(-\left(-6\right)-30)/(2\cdot\:3)=(-30+6)/(6)=-4 \end{gathered}`

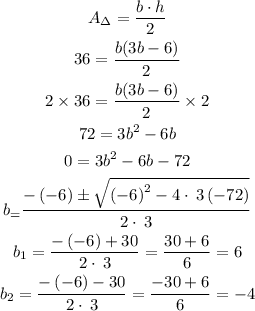
We can discard negative 4 as a measurement for there are no negative measurements. So, we can tell the length of the base is 6 inches

3) Now, let's plug it back into the area formula so that we can get to know the measurement of the height:

`\begin{gathered} A_(\Delta)=(bh)/(2) \\ 36=(6h)/(2) \\ 72=6h \\ 6h=72 \\ 6h=72 \\ (6h)/(6)=(72)/(6) \\ h=12 \end{gathered}`

Thus, the dimensions of that triangle are:

`b=6`