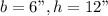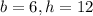
1) Since the height of this triangle is "less than three times the measure of its base" We can call it simply by 3b-6 in which b is the measure of the base.
2) The area is 36 in² so let's plug both pieces of information into the area of a triangle formula and solve it:
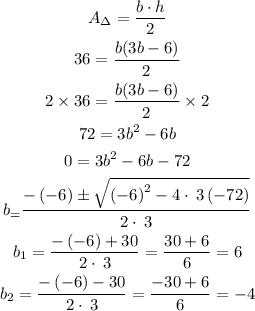
We can discard negative 4 as a measurement for there are no negative measurements. So, we can tell the length of the base is 6 inches
3) Now, let's plug it back into the area formula so that we can get to know the measurement of the height:
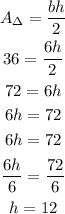
Thus, the dimensions of that triangle are: