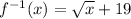Given:
There are given that the function:
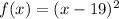
Step-by-step explanation:
According to the question:
We need to find the inverse of the function.
Then,
To find the inverse, first exchange f(x) into y:
So,
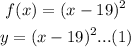
Then,
We need to exchange x into y:
So,
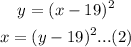
Then,
We need findthe value for y:
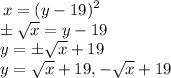
Then,
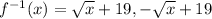
Final answer:
Hence, the inverse of the given function is show below: