Question

Can someone PLEASE explain how to simplify square roots with variables and eexponents in them?? I'd also be thankful if you explained step-by-step how to

solve (16x^4)^3/2 and how to simplify 3y^4/3 times 3yx^1/2? I have to do a retake on my math test and I REALLY need help!

Answer 1

x^a/b is
`\sqrt[b]{x^a}` . The way I memorise that is x^1/3 is the cubic root of x. Do you get it? In that case, x is raised to a power of 1 and the cubic root is practically has a power of 3.
In your example,


`\sqrt[ (3)/(2) ]{16 x^4}` is practically square rooting each term then cubing them individually. Remember when square-rooting any index you halve it. I'll elaborate:


`√(x^4)` =
`x^(2)`

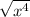
`√(16)` = 4
Then cube each,

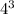
`4^3` = 64
and
`( x^(2) )^3` =
`x^(6)`

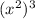
As for the 2nd part: you must use the rules of indices.

`x^(a) * x^(b) = x^(a+b)`
So breaking the question up:

3 * 3 = 9

`x^{ (1)/(2) }` stays as is since the 2nd term does not contain x
now:

`y^{ (4)/(3) } * y^(1) = y^{ (4)/(3) + 1 } = y^{ (4)/(3) + (3)/(3) } = y^{ (7)/(3) }`
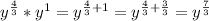
This makes your final answer look like this:

`9 x^{ (1)/(2) } y^{ (7)/(3) }`

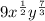
I hope that helped and good luck in your test!