Question

Find the domain of the function f(x)=
`√(x^3-16x)` . What is the least value of x in the domain?

Least Value=

Answer 1

Please check the explanation.

Explanation:

Given the function

`f\left(x\right)=√(x^3-16x)`

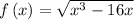
We know that the domain of the function is the set of input or arguments for which the function is real and defined.

In other words,

• Domain refers to all the possible sets of input values on the x-axis.

Now, determine non-negative values for radicals so that we can sort out the domain values for which the function can be defined.

`x^3-16x\ge 0`

as x³ - 16x ≥ 0

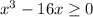
`\left(x+4\right)\left(x-4\right)\ge \:0`

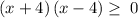
Thus, identifying the intervals:

`-4\le \:x\le \:0\quad \mathrm{or}\quad \:x\ge \:4`

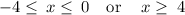
Thus,

The domain of the function f(x) is:

`x\left(x+4\right)\left(x-4\right)\ge \:0\quad :\quad \begin{bmatrix}\mathrm{Solution:}\:&\:-4\le \:x\le \:0\quad \mathrm{or}\quad \:x\ge \:4\:\\ \:\mathrm{Interval\:Notation:}&\:\left[-4,\:0\right]\cup \:[4,\:\infty \:)\end{bmatrix}`

And the Least Value of the domain is -4.