We are going to find the coordinates of the points A'B', which are given by the dilation of AB about the point (5,5) with a scale factor of 2.
For doing so, we will determine the distance between the points A and (5,5), and we will multiply it by 2 (the scale factor). This will be the distance between A' and (5,5). We will do the same between the point B and (5,5).
As the lines x=5 and y=5 are perpendicular, the angle BPA is right (where P is the point (5,5)), we can find the distance of the point A'B' using the Pythagorean Theorem.
Now, we find the distance between A and P:
![\begin{gathered} d(A,P)=\sqrt[]{(5-5)^2+(2-5)^2} \\ =\sqrt[]{0^2+(-3)^2} \\ =\sqrt[]{3^2} \\ =3 \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/high-school/vsfcq5f8w4pa0laqjqxi.png)
And the distance between B and P:
![\begin{gathered} d(B,P)=\sqrt[]{(1-5)^2+(5-5)^2} \\ =\sqrt[]{(-4)^2+0^2} \\ =\sqrt[]{16} \\ =4 \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/high-school/nuuk08wr6dczg2wiqzr0.png)
Multiplying by the scale factor we obtain:
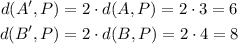
And using the Pythagorean Theorem we obtain:
![\begin{gathered} d(A^(\prime),B^(\prime))=\sqrt[]{d(A^(\prime),P)^2+d(B^(\prime),P)^2} \\ =\sqrt[]{6^2+8^2} \\ =\sqrt[]{36+64} \\ =\sqrt[]{100} \\ =10 \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/high-school/hg6h2zgumu8sollu5uur.png)
This means that the length of the dilation of AB will be 10.