Answer:

Explanation:
Multiply out
 in order to find out which expression it is equivalent to.
in order to find out which expression it is equivalent to.
1) Since the whole quantity is squared, write it out as
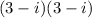 .
.
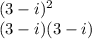
2) Multiply binomials by using the FOIL method. Multiply the terms that are listed first in each binomial, then the ones that are listed outermost when looking at both binomials, then innermost, and finally the last terms listed in each binomial. Simplify and combine like terms.
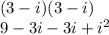

3)
 , so
, so
 must be
must be
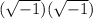 . Thus,
. Thus,
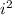 is equivalent to -1. Knowing this, simplify and combine like terms.
is equivalent to -1. Knowing this, simplify and combine like terms.
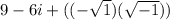

Thus, it is equivalent to
 .
.