Question

46°

7 8
T
E
8
15
10
6
29°
S
20
Given ASTU and ADEF,
what is mZD? what is m/T?
Please help

Answer 1

m ∠D = 29°

m ∠T = 105°

Explanation:

Given: ΔSTU and ΔDEF

To find: m ∠D and m ∠T

Solution:

According to SSS similarity criteria,

two triangles are said to be similar if their corresponding sides are proportional.

In ΔSTU and ΔDEF,

`(ST)/(DE)=(15)/(6)=(5)/(2) \\\\(TU)/(EF)=(10)/(4)=(5)/(2)\\\\(SU)/(DF)=(20)/(8)=(5)/(2)`

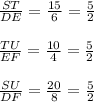
So,

`(ST)/(DE)=(TU)/(EF)=(SU)/(DF)=(5)/(2)`

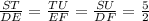
Therefore,

ΔSTU ≈ ΔDEF

If two triangles are similar then measure of their corresponding angles are equal.

m ∠D = m ∠S = 29°

m ∠U = m ∠F = 46°

In ΔSTU,

m ∠S + m ∠T + m ∠U = 180°

29° + m ∠T + 46° = 180°

75° + m ∠T = 180°

m ∠T = 180° - 75° = 105°

(According to angle sum property of a triangle, sum of measures of angles of a triangle is equal to 180°)