We have the next equation
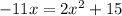
First we need o make the equation equal to zero
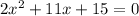
we have a quadratic equation,we will have 2 solutions, so we will use the general formula to find the solutions to this equation
![x_(1,2)=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/zndalnwykxb6ptn1p38z.png)
in our case
a=2
b=11
c=15
![x_(1,2)=\frac{-11\pm\sqrt[]{11^2-4(15)(2)}}{2(2)}_{}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/high-school/rwgw7rmjbe3020zygoxd.png)
![x_(1,2)=\frac{-11\pm\sqrt[]{121-120}}{4}=(-11\pm1)/(4)](https://img.qammunity.org/qa-images/2023/formulas/mathematics/high-school/lxqbq94n0a1qavbqn7kf.png)
for the first solution
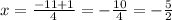
for the second solution
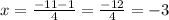
the solutions to the equation given is
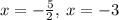
the correct choices are B. and C.