Question

43. Which of the following are solutions to the equation -11x = 2x^2 + 15? Select all that apply. A. -5B. -3C. -5/2D. 5/2E. 3F. 5

Answer 1

We have the next equation

`-11x=2x^2+15`

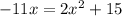
First we need o make the equation equal to zero

`2x^2+11x+15=0`

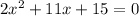
we have a quadratic equation,we will have 2 solutions, so we will use the general formula to find the solutions to this equation

`x_(1,2)=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}`

in our case

a=2

b=11

c=15

`x_(1,2)=\frac{-11\pm\sqrt[]{11^2-4(15)(2)}}{2(2)}_{}`
`x_(1,2)=\frac{-11\pm\sqrt[]{121-120}}{4}=(-11\pm1)/(4)`

for the first solution

`x=(-11+1)/(4)=-(10)/(4)=-(5)/(2)`

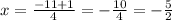
for the second solution

`x=(-11-1)/(4)=(-12)/(4)=-3`

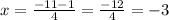
the solutions to the equation given is

`x=-(5)/(2),\: x=-3`

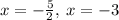
the correct choices are B. and C.