Question

A 20-ounce candle is expected to burn for 60 hours. A 12-ounce candle is expected to burn for 36 hours. Assuming the variables are directly related, how many hours would a 9-ounce candle be expected to burn? 18

Answer 1

Because the ratio for both candles is 20/60 or 1/3 then take the number of ounces the candle has and divide by 1/3. In expression: 9 / 1/3 => 9 * 3 = 18

Answer 2

Answer: A 9-ounce candle is expected to burn for 27 hours.

Step-by-step explanation: Given that a 20-ounce candle is expected to burn for 60 hours and a 12-ounce candle is expected to burn for 36 hours.

If the variables are directly related, we are to find the number of hours that a 9-ounce candle is expected to burn.

Let, x represents the number of ounces of the candle and y represents the corresponding number of hours for which it burns.

Then, since the variables are directly related, the graph will be a straight line.

And, the two points (x, y) = (20, 60) and (12, 36) lies on the line.

So, the slope of the line will be

`m=(36-60)/(12-20)\\\\\\\Rightarrow m=(-24)/(-8)\\\\\Rightarrow m=3.`

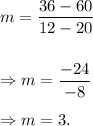
Therefore, the equation of the line is

`y-36=m(x-12)\\\\\Rightarrow y-36=3(x-12)\\\\\Rightarrow y=3x.`

So, if x = 9, then

`y=3*9=27.`

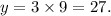
Thus, a 9-ounce candle is expected to burn for 27 hours.