To find the exact coordinates of the point where the diagonals intersect find the equation of each diagonal and then find the solution (where the lines cross each other)
Slope:

For the diagonal that passes for points D ( 0 , 0 ) and B ( 8 , 4)
Slope:
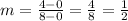
y-intrpcet (b):
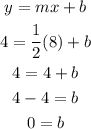
Equation:

For the diagonal that passes for points A ( 1, 5) and C (6 , 2)
Slope:
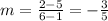
y-intercept (b):
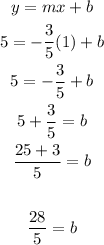
Equation:
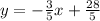
-----------------------------
You have the next sytem of equations:
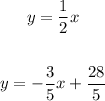
To solve:
1. Substitute the value of y in the second equation for the one in the first equaion:
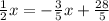
2. Solve for x:
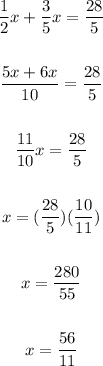
3. Use the value of x to find the value of y:
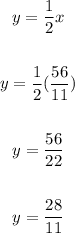
Then, the point where the diagonas intersect is (56/11, 28/11) approximately (5.091,2.545)
