Question

The 8th grade classes at Falling Creek Middle School and Brookville Middle School planned separate trips to Busch Gardens. The class at FCMS rented and filled 14 vans and 10 buses with 752 students. BMS rented and filled 7 vansſand 8 buses with 526 students. Each van and each bus carried the same number of students. Find the number of students in each van and each bus. Write your answer as an ordered pair. ex. (x,y)

Answer 1

Let 'x' be the number of students in vans and let 'y' be the number of students in buses.

Given the information on the problem, we can write the following system of equations:

`\begin{gathered} 14x+10y=752 \\ 7x+8y=526 \end{gathered}`

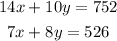
notice that the first equation represents the number of students for FCMS and the second represents the number of students for BMS.

Then, we can multiply the second equation by -2 to get the following:

`\begin{gathered} -2\cdot(7x+8y=526) \\ \Rightarrow-14x-16y=-1052 \end{gathered}`

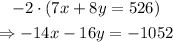
if we add this equation together with the first equation of the system, we have:

`\begin{gathered} 14x+10y=752 \\ -14x-16y=-1052 \\ ------------- \\ -6y=-300 \\ \Rightarrow y=(-300)/(-6)=50 \\ y=50 \end{gathered}`

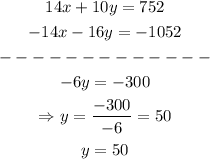
we have that y = 50, now we can use this value to find x on the first equation:

`\begin{gathered} 14x+10(50)=752 \\ \Rightarrow14x=752-500=252 \\ \Rightarrow x=(252)/(14)=18 \\ x=18 \end{gathered}`

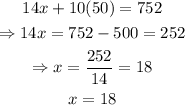
thus, each van was filled with 18 students and each bus was filled with 50 students. The solution of the system is (18,50)