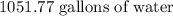Step 1
The circular hot tube is in the shape of a cylinder. Therefore its volume will be;
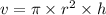
where;
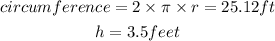
Find r, using the circumference
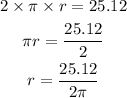
Step 2
Find the volume of the hot tube at 100%
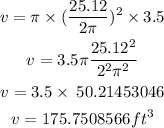
Step 3
Find the recommended capacity which is 80% full
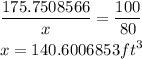
Note; 1 Cubic foot=7.48052 gallons of water. Therefore, the water Rita should put in the hot tub will be;
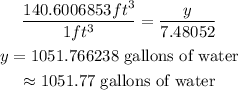
Answer;