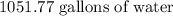Question

Rita has a circular hot tub . The hot tub has a circumference of 25.12 feet . It is 3.5 feet deep. c. The hot tub manual recommends filling the hot tub to 80% of its full capacity. Howmuch water should Rita put in the hot tub in order to follow the recommendation?

Answer 1

Step 1

The circular hot tube is in the shape of a cylinder. Therefore its volume will be;

`v=\pi* r^2* h`

where;

`\begin{gathered} circumference=2*\pi* r=25.12ft \\ h=3.5feet \end{gathered}`

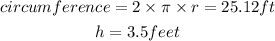
Find r, using the circumference

`\begin{gathered} 2*\pi* r=25.12 \\ \pi r=(25.12)/(2) \\ r=(25.12)/(2\pi) \\ \end{gathered}`

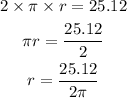
Step 2

Find the volume of the hot tube at 100%

`\begin{gathered} v=\pi*((25.12)/(2\pi))^2*3.5 \\ v=3.5\pi(25.12^2)/(2^2\pi^2) \\ v=3.5*\:50.21453046 \\ v=175.7508566ft^3 \end{gathered}`

Step 3

Find the recommended capacity which is 80% full

`\begin{gathered} (175.7508566)/(x)=(100)/(80) \\ x=140.6006853ft^3 \\ \end{gathered}`

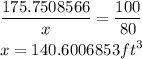
Note; 1 Cubic foot=7.48052 gallons of water. Therefore, the water Rita should put in the hot tub will be;

`\begin{gathered} (140.6006853ft^3)/(1ft^3)=(y)/(7.48052) \\ y=1051.766238\text{ gallons of water} \\ \approx1051.77\text{ gallons of water} \end{gathered}`

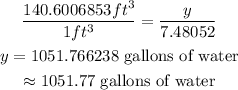
Answer;

`1051.77\text{ gallons of water}`