Question

A radioactive isotope is known to have a half-life of 14 days. How many grams of a 500 gram sample of the isotope will remain after 5 weeks?

Answer 1

Exponential Decay

The rate of decay of radioactive material is proportional to its actual mass. When solving the resulting equation, we get the mathematical model as follows:

`m(t)=m_oe^{-\lambda\mathrm{}t}`

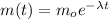
Where mo is the initial mass, λ is a constant, and t is the time.

The half-life time is the time it takes for the initial mass to be halved, i.e., the remaining mass is mo/2. Substituting into the formula for t=14 days:

`(m_o)/(2)=m_oe^(-14\lambda)`

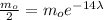
Simplifying by mo and solving for λ:

`\begin{gathered} (1)/(2)=_{}e^(-14\lambda) \\ \ln (1)/(2)=-14\lambda \\ \lambda=(\ln 2)/(14) \\ Calculate\colon \\ \lambda=0.04951 \end{gathered}`

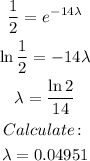
Now our model is complete:

`m(t)=m_oe^(-0.04951t)`

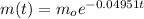
Now we are given the initial mass of a sample mo = 500 grams. It's required to calculate the remaining mass after t = 5 weeks = 5*7 = 35 days.

Substitute values:

`\begin{gathered} m(35)=500e^(-0.04951\cdot35) \\ \text{Operating:} \\ m(35)=500\cdot0.17678 \\ \boxed{m(35)=88.39} \end{gathered}`

Approximately 88 grams of the sample will remail after 5 weeks