Answer:
Please check the attached diagram.
Explanation:
The slope-intercept form of the line equation
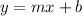
where
- m is the rate of change or slope
Analysis of y = - 3x + 2
Given the linear function
y = - 3x + 2
comparing with the slope-intercept form y = mx+b
The slope m = -3
The negative slope indicates that as the line on the line graph moves from left to right, the line falls.
In other words, the negative slope indicates that when x increases, y decrease, and vise versa.
Please check the attached graph of the function y = - 3x + 2. It is clear that when x increases, y decreases, hence the line falls when the graph of the line moves from left to right.
The red line graph represents the linear function y = - 3x + 2.
Analysis of y = 4x + 2 (When -3 is replaced by 4)
Now, when we replace -3 by 4 in the equation y = - 3x + 2, the equation becomes
y = 4x + 2
comparing with the slope-intercept form y = mx+b
The slope m = 4
The positive slope indicates that as the line on the line graph moves from left to right, the line rises.
In other words, the positive slope indicates that when x increases, y also increases, and vise versa.
Please check the attached graph of the function y = 4x + 2. It is clear that when x increases, y increases, hence the line rises when the graph of the line moves from left to right.
The blue line graph represents the linear function y = 4x + 2.
Analysis of y = 2 (When -3 is replaced by 0)
Given the equation
y = - 3x + 2
If we replace -3 by 0, the equation becomes
y = 0x + 2
y = 2
In other words, y = 2 represents a horizontal line because the horizontal line is of the form
y = k
where k is the y-intercept
here k = 2 is the y-intercept of the line y = 2.
Thus, slope zero means the value of y does not change no matter what we take or change the x-value.
The graph of line y = 2 is also attached which represents a horizontal line with slope 0 and y-intercept 2.
The green line graph represents the linear function y = 2.
Please check the graphs of all the lines.