We are given the following endpoints
A (2, 4) and B (17, 14)
We need to find point P such that the segment is in the rato of 2:3
Total segments = 2+3 = 5
The x-coordinate of the point P is given by
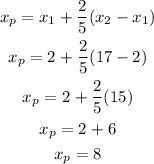
The y-coordinate of the point P is given by
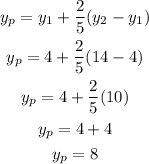
Therefore, the point P is (8, 8)