Question

In 2004, a school population was 1001. By 2008 the population had grown to 1697. Assume the population is changing linearly.How much did the population grow between the year 2004 and 2008? It grew by Answer people.How long did it take the population to grow from 1001 students to 1697 students?Answer yearsWhat is the average population growth per year? Answer per yearWhat was the population in the year 2000? AnswerpeopleFind an equation for the population, P, of the school t years after 2000. P(t)=AnswerUsing your equation, predict the population of the school in 2011. In the year 2011 there will be Answer people.

Answer 1

We are given that the population in 2004 was 1001 and by 2008 it was 1697. We are assuming linearity.

To determine how much the population grew between 2004 and 2008 we need to determine the difference of the populations for each year. This is:

`\Delta P=1697-1001=696`

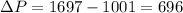
Therefore, the population grew by 696 people

Where:

`\Delta P=Population\text{ growth}`

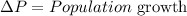
Now we are asked how long did it take this population to grow that amount. To do that we will determine the difference between each year, that is:

`\Delta t=2008-2004=4`

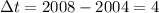
Therefore, there is a difference of 4 years.

To determine the average growth per year, we will find the quotient between the population growth and the time difference, we will call this quantity "m", we get:

`m=(\Delta P)/(\Delta t)`

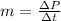
Substituting the values:

`m=(696)/(4)=174`

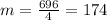
Therefore, the average population growth per year is 174 people per year.

To determine the population in year 200 we need to have into account that since the population behaves linearly this means that every four years the population will add 696 people, as we determined in the first part for years 2004 and 2008. Therefore, the population in 2000 must be the population in 2004 minus the amount the population grows, therefore:

`P_(2000)=1001-696=305`

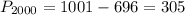
Therefore, the population in 2000 is 305 people.

A linear equation must be of the form:

`P(t)=mt+b`

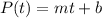
Where "m" is the slope or the average growth of people per year. "b" is the intercept or the number of people in the initial year. Since the initial year is 2000 we have:

`P(t)=174t+305`

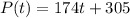
Finally, to determine the population in 2011 we need to have into account that from 2000 to 2011 there are 11 years, therefore:

`\begin{gathered} P(11)=174(11)+305 \\ \end{gathered}`

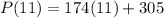
Solving the operations:

`P(11)=2219`

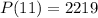
Therefore, the population in 2011 is 2219 people.