Question

A plane flying due west at 120 m/sec is blown due south at 54 m/sec. by a strong wind. Find the plane’s resultant velocity and direction angle as a degree.

velocity = ___ m/sec (round answer to nearest whole number)


Direction angle = ____ ° (round answer to nearest whole number)

Answer 1

1) Velocity = 132 m/sec

2) Direction angle = 24° South of West

Explanation:

1) The speed with which the plane is flying,
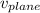`v_(plane)` = 120 m/sec

The direction in which the plane is flying = Due West

The speed of the blowing strong wind,
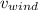`v_(wind)` = 54 m/s

The direction of the strong wind = Due South

The vector form of the given velocities are;

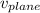`v_(plane)` = -120·i

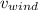`v_(wind)` = 54·j

The resultant velocity in vector format,
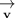`\underset{\textbf{v}}{\rightarrow}` is given as follows;

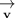`\underset{\textbf{v}}{\rightarrow}` = -120·i + 54·j

Therefore, the magnitude of the resultant velocity,
`\left |\underset{v}{\rightarrow} \right |`, is given as follows;

`\left |\underset{v}{\rightarrow} \right |` = √((-120)² + (54)²) = 131.590273197

∴ The magnitude of the plane's resultant velocity,
`\left |\underset{v}{\rightarrow} \right |` ≈ 132 m/sec, when rounded to the nearest whole number

2) The direction angle of the plane's resultant velocity, θ, is given as follows;

`\theta = arctan \left ( (\left |v_(wind)\right |)/(\left |v_(plane)\right |) \right)`

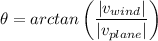
Therefore, by substituting the known values, we have;

`\theta = arctan \left ( -(54)/(120) \right) = -24.227745317954169522385424019918 ^(\circ)`

∴ By rounding to the nearest whole number, the direction angle of the plane's resultant velocity = θ ≈ -24° = 204° which is 24° South of West.