Answer:
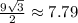 square units.
square units.
Explanation:
We have been given that AB is tangent to circle C. We are asked to find the area of triangle ABC.
We know that tangent is perpendicular to radius of circle, therefore, measure of angle A is 90 degrees.
Our given triangle is 30-60-90 triangle, so length of side AB (opposite to 60 degree) will be
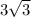 .
.
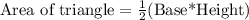
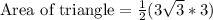
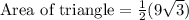
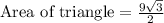
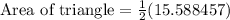
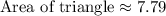
Therefore, the area of the triangle is
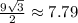 square units.
square units.