Question

The height of water shooting from a fountain is modeled by the function f(x) = −4x2 + 24x − 29 where x is the distance from the spout in feet. Complete the square to determine the maximum height of the path of the water.

−4(x − 3)2 − 29; The maximum height of the water is 3 feet.

−4(x − 3)2 − 29; The maximum height of the water is 29 feet.

−4(x − 3)2 + 7; The maximum height of the water is 7 feet.

−4(x − 3)2 + 7; The maximum height of the water is 3 feet.

Answer 1

Option 3 -
`y= -4(x-3)^2+7`; The maximum height of the water is 7 feet.

Explanation:

Given : The height of water shooting from a fountain is modeled by the function
`f(x) = -4x^2+24x-29` where x is the distance from the spout in feet.

To find : Complete the square to determine the maximum height of the path of the water.

Solution :

`f(x) = -4x^2+24x-29`

`f(x) = -4(x^2-6x)-29`

Completing the square by adding and subtracting
`((6)/(2))^2=3^2=9` in the bracket,

`f(x) = -4(x^2-6x+9-9)-29`

`f(x) = -4((x-3)^2-9)-29`

`f(x) = -4(x-3)^2+36-29`

`f(x) = -4(x-3)^2+7`

The general vertex form is
`y=a(x-h)^2+k`

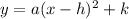
On comparing,

a=−4, h=3, k=7

The maximum height of the water is given by y-intercept i.e. k,

The maximum height of the water is 7 feet.

Therefore, Option 3 is correct.

Answer 2

Below is the solution:

f(x)=−4(x2−6x+9−9)−29

(x2−6x+9)=(x−3)(x−3)

f(x)=−4((x−3)2−9)−29

f(x)=−4(x−3)2−4(−9)−29

f(x)=−4(x−3)2+36−29

f(x=−4(x−3)2+7

f(x)=−4(x−3)2+7

That's the equation we got by completing the square.

y=a(x−h)2+k

That's the formula of a parabola in "vertex" form. Notice the similarity? The two are equal if we say

y=f(x)

a=−4

h=3

k=7

Therefore the answer is C, −4(x − 3)2 + 7; The maximum height of the water is 7 feet.