The correct answers are:
(1)
 (Option C)
(Option C)
(2)
 (Option A)
(Option A)
(3)
 is a polynomial (Option A)
is a polynomial (Option A)
Explanations:
(1) Given Expression:

Now simplify as follows:
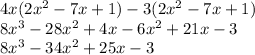
Therefore, the correct answer is
 (Option C)
(Option C)
(2) Given Expression:
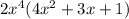
Now simplify as follows:
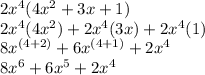
Therefore, the correct answer is
 (Option A)
(Option A)
(3) Given Data:
Polynomial one: 4x + 6
Polynomial two:
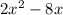
First multiply both polynomials:

Now as we can see, if we multiply two polynomials, the resultant expression is also a polynomial. Therefore, it does demonstrate the closure property (closed set). Hence, the correct answer is
 (Option A)
(Option A)