Question

Simplify the expression. 12 p 5
A. 11,880
B. 95,040
C. 1,235,520
D. 7,920

Answer 1

The number of permutations of 12 different items taken 5 at a time is:

`12P5=(12!)/(7!)=95,040`
So the correct answer is B. 95,040

Answer 2

Option B is correct.

Explanation:

We have been given an expression:

`^(12)P_5`

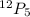
Above expression is of permutation we have a formula to solve the permutation which is:

`^n{P}_r=(n!)/((n-r)!)`

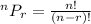
Here, n=12 and r=5

On substituting the values in the formula we get:

`^12{P}_5=(12!)/((12-5)!)` (1)

And also:
`n!=n(n-1)(n-2)....1`

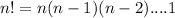
Equation 1 becomes after first step of simplification:

`(12\cdot11\cdot10\cdot9\cdot8\cdot7!)/(7!)`

Common term from numerator and denominator which is 7! will get cancelled we get:

`12\cdot11\cdot10\cdot9\cdot8`

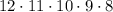
After simplification we get:

95040

Therefore, Option B is correct