Question

8. Fig. 4.1 shows a heavy ball B of weight W suspended from a fixed beam by two ropes P and Q.

P and Q are both at an angle of 45° to the horizontal. The tensions in P and Q are each 30 N.
a. In the space below, draw a scale diagram to find the resultant of the tensions
in P and Q. Use a scale of 1.0cm to represent 5.0 N. Label the forces and show
their directions with arrows.

Answer 1

The resultant tension of the two ropes is approximately 42.4 N

The length of the line representing the resultant tension is approximately 8.48 cm

Please find included with the answer the scale drawing created with Microsoft Word

Step-by-step explanation:

The given parameters are;

The tension in rope P,
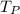`T_P` = 30 N

The tension in rope Q,
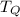`T_Q` = 30 N

The angle the rope, 'P', makes with the horizontal = 45°

The angle the rope, 'Q', makes with the horizontal = 45°

The scale factor of the scale diagram, S.F. = 5.0 N/cm

By the resolution of forces at equilibrium, we have;

The sum of the vertical forces,
`\Sigma F_y` =
`T_P_y` +
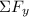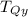`T_Q_y` + W = 0

∴ W = -(
`T_P_y` +
`T_Q_y`)

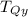W = -(30 × sin(45°) + 30 × sin(45°)) = -42.4264068712

The weight of the heavy ball, W ≈ 42.4 N acting downwards

The sum of the horizontal forces,
`\Sigma F_x` =
`T_P_x` +
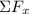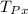`T_Q_x` = 0

The length of the resultant force, W = W/(S.F.) ≈ 42.4 N/(5.0 N/cm) = 8.48 cm

The drawing of the vectors using the scale factor of 5.0 N/cm is created using Microsoft Word is included