Question

Consider the curves in the first quadrant that have equations y=Aexp(6x) where A is a positive constant. Different values of A give different curves. The curves form a family, F. Give a formula g(y) for the slope at (xy) of the member of F that goes through (xy). The formula should not involve A or x.

Answer 1

then the derivative of Ae6x is 6Ae6x replace x by 16ln(yA) and get 6y
i found this somewhere else i didnt do the work but i believe its right

Answer 2

`y'=6y`

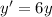
Explanation:

Given is the curve exponential in the I quadrant

`y=Ae^(6x)`

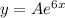
where A is positive

For different values of A, we have different curves which together form a family of curves

The differential equation to be formed using slope and x,y would be as follows:

Differentiate the given equation wrt x

`y' =6Ae^(6x)`

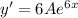
This is the slope

Eliminate A to get

slope =

`y'=6y`

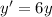
This would be the formula for slope without A or x in it