Answer: The correct option is (a) 12.
Step-by-step explanation: We are given to find the number of permutations that exists for the letters a, b, c and d taking two at a time.
We know
The number of permutations of 'n' different things taking 'r' ('r' less than or equal to 'n') at a time is given by the formula:
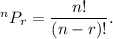
In the given case, there are 4 different letters and we are to take two at a time, so
n = 4 and r = 2.
Therefore, the number of permutations will be
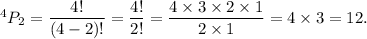
Thus, there are 12 permutations that exists.
Option (a) is correct.