Question

What is true about the solutions of a quadratic equation when the radicand of the quadratic formula is a positive number that is not a perfect square?

A. No real solutions

B. Two identical rational solutions

C. Two different rational solutions

D. Two irrational solutions

Answer 1

Option D Two irrational solutions

Explanation:

Any quadratic equation of the form would be

`ax^2+bx+c=0`

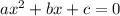
We can solve this by completion of squares.

Multiply by 4a

`4a^2x^2+4abx+4ac=0\\(2ax+b)^2-b^2+4ac=0\\(2ax+b)^2=b^2-4ac\\2ax+b=√(b^2-4ac) \\x=(-b+or -√(b^2-4ac) )/(2a)`

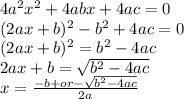
Thus we find the solution as above

The square root if 0 we have two equal solutions

If perfect square we have two rational solutions

But here given that the discriminant b^2-4ac is positive but not perfect square

Hence the square root would be irrational thus the solution also would be irrational

Hence answer is

Option D Two irrational solutions

Answer 2

The answer that is true about the solution of a quadratic equation when the radicand of the quadratic formula is a positive number that is not a perfect square is two irrational solutions. The correct answer is D.