Question

Solve on the interval [0, 2Pi):

1 + cos(theta) = (sqrt(3)+2)/2
A. Pi/6 , 5Pi/6
B. Pi/3 , 5Pi/3
C.Pi/6 , 11Pi/6
D. 7Pi/6, 11Pi/6

Answer 1

Option C is right

Explanation:

`1+cos\theta =(√(3)+2 )/(2) =(√(3) )/(2) +1`

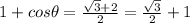
Now we cancel 1 and get

`cos\theta =(√(3) )/(2)`

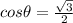
The solutions would be positive for cos hence the angle lies in I quadrant, IV quadrant.

In I quadrant angle satisfying in the I quadrant, is 30 degrees, pi/6

In IV quadrant this would be 2pi-pi/6 = 11pi/6

Hence solution is

pi/6, 11 pi/6

OPtionC

Answer 2

1 + cos t = ( √3 + 2 ) /2
cos t = ( √3 + 2 ) / 2 - 1
cos t = ( √3 + 2 - 2 ) / 2
cos t = √3/2
t 1 = π/6, t 2 = 11π/6
Answer: C ) π/6, 11π/6.