Question

A motor boat traveled 135 miles down a river in 18 hours but going back upstream, it took 30 hours due to the current. Find the rate of the motor boat in still water and the rate of the current. (Round to the nearest tenth if necessary.)

Answer 1

Step 1:

Let the rate(speed) of motor boat = m

Let the rate(speed) of current = n

Step 2:

Distance = Speed X Time

Time = 18hour for down a river

Total distance for flowing downward = 135

`\begin{gathered} 18m\text{ + 18n = 135} \\ 2m\text{ + 2n = 15} \end{gathered}`

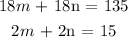
Total distance for flowing upstream due to current = 135

`\begin{gathered} 30m\text{ - 30n = 135} \\ 2m\text{ - 2n = 9} \end{gathered}`

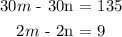
Step 3:

Add the first and the second equation.

`\begin{gathered} 2m\text{ + 2n + 2m - 2n = 15 + 9} \\ 4m\text{ = 24} \\ \text{m = }(24)/(4) \\ \text{m = 6 mile/hr} \end{gathered}`

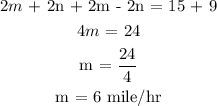
Substitute m in any equation to find n.

`\begin{gathered} 2m\text{ - 2n = 9} \\ 2*\text{6 - 2n = 9} \\ 12\text{ - 2n = 9} \\ 2n\text{ = 12 - 9} \\ 2n\text{ = 3} \\ n\text{ = }(3)/(2) \\ n\text{ = 1.5 miles/hr} \end{gathered}`

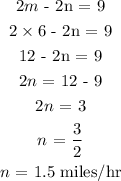
Final answer

Rate of the motor boat in still water m = 6 miles/hr

Rate of the current n = 1.5 miles/hr