Question

Derive the equation of the parabola with a focus at (−7, 5) and a directrix of y = −11.

f(x) = one thirty second (x + 7)2 − 3

f(x) = −one thirty second (x + 7)2 − 3

f(x) = −one thirty second (x − 7)2 − 3

f(x) = one thirty second (x − 7)2 − 3

Answer 1

In this problem, given the focus at (-7,5) and directrix at y = -11. then it is implied that the parabola is facing upwards. The vertex hence is at the middle of the focus and the directrix, hence at (-7, -3). The general formula of the parabola is y-k = 4a  ( x-h)^2. SUbstituting, y + 3 = 1/30 *(x+7)^2. Answer i sA. 

Answer 2

Solution: The correct of option (1).

Step-by-step explanation:

if the parabola is defined by the equation
`(x-h)^2=4p(y-k)` then the focus of parabola is defined by
`f(h,k+p)` and directrix is defined by
`y=k-p`.

The focus is (-7,5), therefore h=-7 and

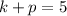`k+p=5` ...(1)

The given directrix is
`y=-11`,

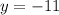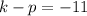`k-p=-11` ....(2)

Add equation (1) and (2),

`2k=-6\\k=-3`

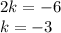
Put
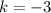`k=-3` in equation (1), we get
`p=8`.

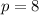Substitute these values in equation
`(x-h)^2=4p(y-k)`.

`(x+7)^2=4(8)(y+3)\\y=(1)/(32)(x+7)^2-3`

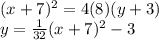
Therefore, the correct option is option (1).