Question

In 1994, the moose population in a park was measured to be 4600. By 1997, the population was measured again to be 4300. The population continues to change linearly.

Find the equation for the moose population, P, in terms of T years since 1990.

P(t)= ___________

What does your model predict the moose population to be in 2008?

____________________

Answer 1

`p = -100t + 5000`

The model predicts 3200 moose in 2008

Explanation:

Given

In 1990, year (i.e p) would be 0

So:

In 1994:

`(t_1,p_1) = (4,4600)`

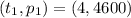
In 1997 (3 years later):

`(t_2,p_2) = (7,4300)`

To get the equation, we first solve for the slope (m)

`m = (p_2 - p_1)/(t_2 - t_1)`

Substitute values for the p's and t's

`m = (4300 - 4600)/(7 - 4)`

`m = (-300)/(3)`

`m = -100`

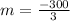
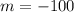
The equation is then calculated using:

`p - p_1 = m(t - t_1)`

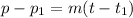
Substitute values for p1, m and t1

`p - 4600 = -100(t - 4)`

Open bracket

`p - 4600 = -100t + 400`

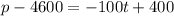
Make p the subject

`p = -100t + 400+4600`

`p = -100t + 5000`

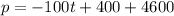
In 2008:

The value of t would be 18 (i.e. 2008 - 1990)

Substitute 18 for t in
`p = -100t + 5000`

`p = -100* 18 + 5000`

`p = -1800 + 5000`

`p = 3200`

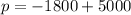
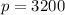
The model predicts 3200 moose in 2008