Question

Calculate the area of triangle QRS with altitude ST, given Q (0, 5), R (−5, 0), S (−3, 4), and T (−2, 3).

A- 6.2 square units

B- 7 square units

C- 5.9 square units

D- 5 square units

Answer 1

The correct answer among the choices provided is option D. The area of triangle QRS with altitude ST is 5 square units. To solve for the area, the distance formula was used. The formula was substituted with the given values, QR=√[(-5-0)²+(0-5)²].

Answer 2

we have that

`Q (0, 5)\\R (-5, 0)\\S (-3, 4)\\T (-2, 3)`

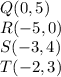
using a graph tool

see the attached figure

the Area of triangle QRS is equal to

`A=(1)/(2)*b*h\\ A=(1)/(2)*RQ*ST`

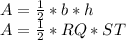
1) Find the distance RQ

Applying the formula of distance

`d=\sqrt{(y2-y1)^(2)+(x2-x1)^(2)}`

`dRQ=\sqrt{(0-5)^(2)+(-5-0)^(2)}`

`dRQ=√((25)+(25))`

`dRQ=√(50) units`

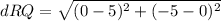
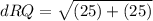
2) Find the distance ST

`dST=\sqrt{(3-4)^(2)+(-2+3)^(2)}`

`dST=√((1)+(1))`

`dST=√(2) units`

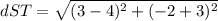
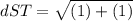
3) Find the area of triangle QRS

`A=(1)/(2)*RQ*ST\\\\ A=(1)/(2)*√(50)*√(2) \\\\ A=(1)/(2)*√(100) \\ \\ A=(10)/(2) \\ \\ A=5 units^(2)`

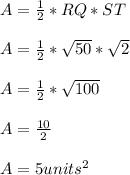
therefore

the answer is the option

D-
`5` square units