Given:
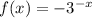
To plot five points on the graph, we input any values of x into the given function.
Example:
Let x=2
So,
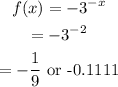
Thus, the point is (2,-1/9).
Let x=1:
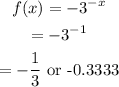
Thus, the point is (1,-1/3).
Let x=0
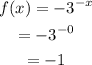
Thus, the point is (0,-1).
Let x=-1
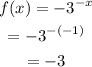
Thus, the point is (-1,-3).
Let x=-0.5
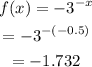
Thus, the point is (-0.5,-1.732).
Then, to get the asymptote, we use