Question

Q1. Which system of equations is represented by the graph?

a line is graphed through points negative 6 comma 7 and negative 1 comma 2. It intersects a parabola that opens up at these two points.

A. y = x^2 − 6x − 7
x − y = 1

B. y = x^2 − 6x + 7
x + y = −1

C. y = x^2 + 6x − 7
x − y = 1

D. y = x^2 + 6x + 7
x + y = 1

Answer 1

The correct option is D.

Explanation:

From the given graph it is noticed that the line and parabola intersect each other at points (-6,7) and (-1,2). It means each equation of the system must be satisfied by these points.

If a line passing through two points, then the equation of line is

`y-y_1=(y_2-y_1)/(x_2-x_1)(x-x_1)`

The equation of line is

`y-7=(2-7)/(-1-(-6))(x-(-6))`

`y-7=-(x+6)`

`y-7=-x-6`

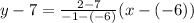
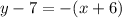
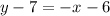
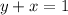`y+x=1` .... (1)

Therefore the equation of line is
`y+x=1`.

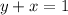The standard form of the parabola is

`y=a(x-h)^2+k`

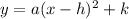
Where (h,k) is the vertex.

From the graph it is noticed that the vertex of the parabola is (-3,-2).

`y=a(x+3)^2-2`

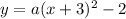
The parabola passing through the point (-1,2).

`2=a(-1+3)^2-2`

`2=4a-2`

`a=1`

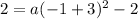
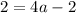
Therefore the equation of parabola is

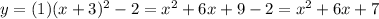`y=(1)(x+3)^2-2=x^2+6x+9-2=x^2+6x+7` .... (2)

So, the system of equations contains equation (1) and (2). Option D is correct.

Answer 2

Let

`A(-6,7)\\B(-1,2)`

we know that

The points A and B must satisfy both equations

we proceed to verify each case

case A)

equation
`1`

`y=x^(2) -6x-7`

check point A

for
`x=-6`

y must be
`7`

substitute

`y=(-6)^(2) -6*(-6)-7`

`y=36+36-7\\ y=65`

`65` is not equal to
`7`

so

The system of equations is not represented by the graph

It is not necessary to check point B

case B)

equation
`1`

`y=x^(2) -6x+7`

check point A

for
`x=-6`

y must be
`7`

substitute

`y=(-6)^(2) -6*(-6)+7`

`y=36+36+7\\ y=79`

`79` is not equal to
`7`

so

The system of equations is not represented by the graph

It is not necessary to check point B

case C)

equation
`1`

`y=x^(2) +6x-7`

check point A

for
`x=-6`

y must be
`7`

substitute

`y=(-6)^(2) +6*(-6)-7`

`y=36-36-7\\ y=-7`

`-7` is not equal to
`7`

so

The system of equations is not represented by the graph

It is not necessary to check point B

case D)

equation
`1`

`y=x^(2) +6x+7`

check point A

for
`x=-6`

y must be
`7`

substitute

`y=(-6)^(2) +6*(-6)+7`

`y=36-36+7\\ y=7`

`7` is equal to
`7`------->is ok

check point B

for
`x=-1`

y must be
`2`

substitute

`y=(-1)^(2) +6*(-1)+7`

`y=1-6+7\\ y=2`

`2` is equal to
`2`----->is ok

equation
`2`

`x+y=1`

check point A

for
`x=-6`

y must be
`7`

substitute

`-6+y=1\\ y=6+1\\ y=7`

`7` is equal to
`7`------->is ok

check point B

for
`x=-1`

y must be
`2`

substitute

`-1+y=1\\ y=1+1\\ y=2`

`2` is equal to
`2`----->is ok

therefore

the answer is the option D

`y=x^(2) +6x+7`

`x+y=1`