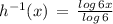Question

What is the inverse of h? h(x) = 6x 1

Answer 1

The inverse of h(x) is
`h^(-1)(x)\,=\,(log\,6x)/(log\,6)`

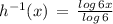
Explanation:

Given: h function, h(x) =
`6^(x-1)`

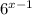
To find: Inverse of h function.

We are given h function in terms of x. So we equate this function with arbitrary element say y, then convert the given function of x in terms of y.

The function we obtained in term of y is the required inverse function of h.

Consider,

y = h(x)

`y\,=\,6^(x-1)`

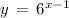
Take log on both sides, we get

`log\,y\,=\,log\,6^(x-1)`

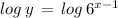
now we use rule of logarithmic function in RHS,
`log\,m^n\,=\,n\,log\,m` , we get

`log\,y\,=\,(x-1)\,log\,6`

`x-1\,=\,(log\,y)/(log\,6)`

`x\,=\,(log\,y)/(log\,6)+1`

`x\,=\,(log\,y+log\,6)/(log\,6)`

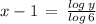
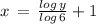
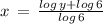
Now using another rule of logarithmic function
`log\,mn\,=\,log\,m+\,log\,n` we get

`x\,=\,(log\,6y)/(log\,6)`

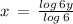
Therefore, The inverse of h(x) is
`h^(-1)(x)\,=\,(log\,6x)/(log\,6)`

Answer 2

h(x) = 6x + 1
y = 6x + 1
6x = y - 1
x = (y - 1)/6

Inverse is h^-1(x) = (x - 1)/6