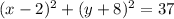Question

write an equation for a circle with a diameter that has endpoints at (8, –9) and (–4, –7). round to the nearest tenth if necessary.

Answer 1

An equation of a circlewith radius r and center (h,k) is in form
`(x-h)^2+(y-k)^2=r^2` Diameter is twice radius so find the distance between the given points and halve it to get radius D=
`\sqrt{( x_(1)-x_(2))^2+(y_(1)-y_(2))^2}` D=
`√(( 8-(-4))^2+(-9-(-7))^2)` D=
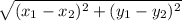
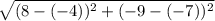
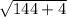
`√(144+4)` D=√148 D=2√37 Halve that R=√37 The center is the midpoint of the 2 points that make up the diameter So find the midpoint of the points (8,-9) and (-4,-7) Midpoint of two points (x1,y1) and (x2,y2) is
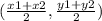
`( (x1+x2)/(2), (y1+y2)/(2))` Midpoint between (8,-9) and (-4,-7) is (2,-8) That is the center of the circle (h,k) so R=√37 (h,k)=(2,-8) So the equation is
`(x-2)^2+(y+8)^2=37`