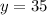Question

How do I find the x and the y

Answer 1

x =22°

y =35°

Explanation:

3x-11 = 2x+11

then x =22°

and 2y = 180-(55+55)

2y = 70

y = 45°

Answer 2

x = 22

y = 35

Explanation:

Because its an isosceles triangle, you know the base angles are equal so:

`3x - 11 = 2x + 11`

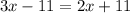
Solving:

subtract 2x from both sides

`x-11=11`

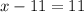
add 11 to both sides

`x = 22`

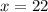
Next, find the angle measures of the two base angles:

`3*22-11\\66-11\\55`

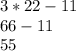
To find y, you know that the interior angles of the whole triangle add up to 180, so you have

`55 + 55 + 2y = 180`

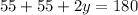
solving,

`110 + 2y = 180`

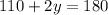
subtract 110 from both sides

`2y = 70`

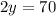
divide both sides by 2

`y = 35`